n-Dimensional Gridmaps: Formulation and Implementation
Contents:
It all started in a cold winter morning, after spending 2 weeks trying to create a hierarchy of C++ classes to implement functions valid to any kind of grid map, it turned out that the best solution were to work with grid indices and forget about coordinates! This way we can parametrize everything. "There should be something on the Internet about this". After a few hours looking for how to extract neighbors of grids with number and size of dimensions not fixed I decided it was time to try it by myself...

FM toolbox test output
Grid maps are extensively used in many different algorithms. Among the different grid map types we are focusing on rectangular (or cubic) grid map with a priori unknown number of dimensions. We are detailing the main problems that arise when working with this type of data structure: extraction and validation of 4-connectivity neighbors for a given cell, conversion from index to coordinates (and vice-versa) and the mathematical generalization to n-dimensional grids. Also, we are detailing a generic implementation available as free software.
In this page I posted a document (and its sources) to understand the mathematical formulation and generalization of n-dimensional grid maps. Also a link to my implementation of a grid map of n dimension is provided. The main characteristics here are that it is easy to use.
Downloads
Source code
- Biicode block: Recommended! Check out my Path Planning tutorial to learn how to use it.
- Github repository: Included in my Fast Marching code.
Generalized neighbors extraction
The formulation for a 2D grid are summarized in the following pixs. Hard to understand if the report has not been read:
For a 2D and 3D grids, neighbors are:
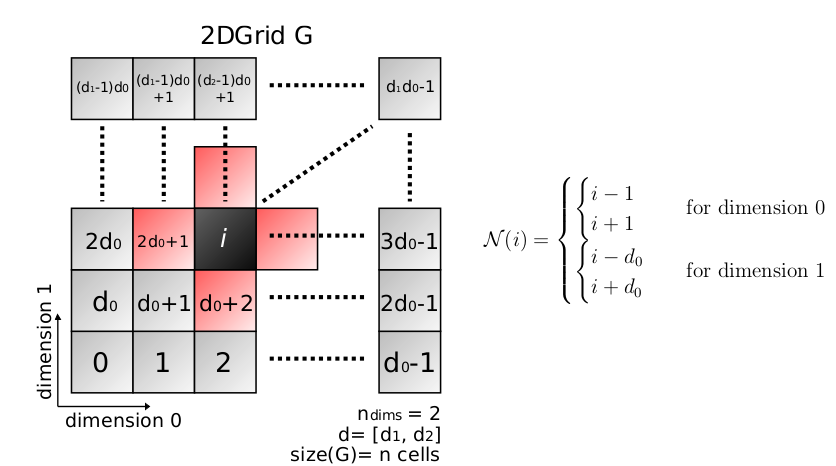
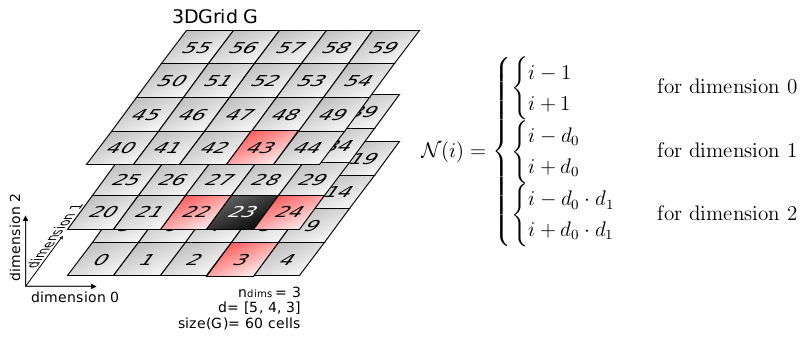
Von-Neumann (4-connectivity) neighbors computation for 2D and 3D grids.
Therefore, for a nD grid:

Von-Neumann (4-connectivity) neighbors computation for nD grids.
Obviously, not all the neighbors are valid since the cell queried can be in an edge or in a corner. In the full report it is described how to generalize the neighbors checking.
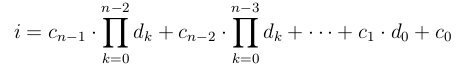
Von-Neumann (4-connectivity) coordinates to index conversion.
Helper functions
Conversion from Coordinates to Index
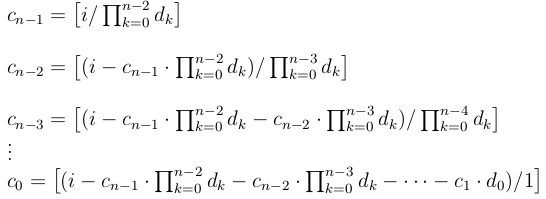
Von-Neumann (4-connectivity) index to coordinates conversion.