JV - Science and stuff.

Fast Marching Method and Fast Marching Square

Contents:

Introduction

Here, I summarize my planning research into path planning based on Fast Marching Method (FMM) and Fast Marching Square (FM2) methods.

Note
Most, if not all, of my algorithms work in any number of dimensions. However, with FMM and FM2 I focus on 2D and 3D. They are really slow in more than 4 dimension.

Fast Marching Methods in Path planning

Originally, FMM was a very efficient way of computing distances fields. A distance field is an scalar field in which any point of the space contains the distance to a given point, taking into account the environment, not just using straight lines. In other words, obstacles have to be avoided. This is done by simulating a wave propagation through the environment. And this wave cannot go through obstacles.

Actually, FMM does not compute distances but arrival times. That is, the time the wave takes to arrive to a given point. For constant velocity it is equivalent to Euclidean distance. However, it becomes really interesting in cases in which the velocity is no constant.

Fast Marching Method

Fast Marching Method. With constant velocity, FMM returns the optimal path in terms of distance.

Fast Marching Square

Now, let us set a velocities map. We will set a relative velocity giving every point in the map a velocity directly proportional to the distance of its closest obstacle. And we will use FMM in order to compute this velocities map (which is, in fact, a distance transform). We will be applying FMM later over this velocities map. Hence the name.

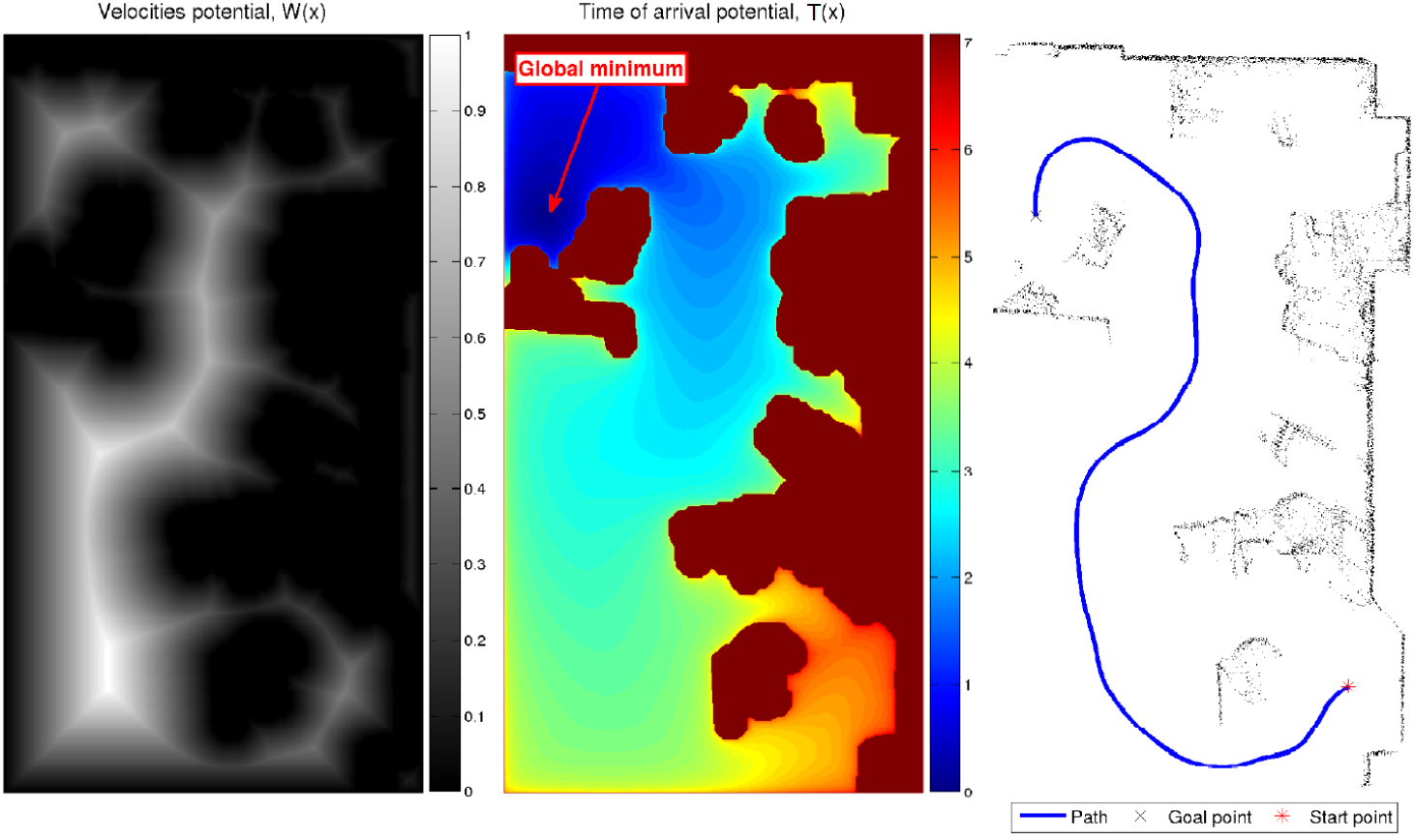
Fast Marching Method

Fast Marching Square. Provides safe, smooths trajectories. In this case, the method provides the optimum time trajectory assuming that the robot is moving at the speed determined by the velocities map.




Application to the ITER project

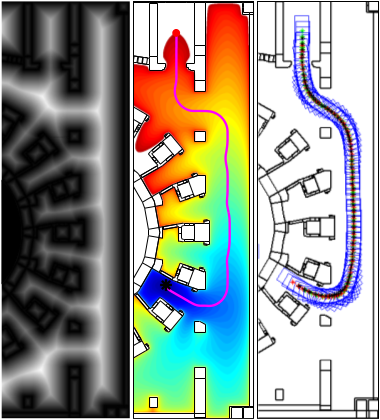
Fast Marching Method

Fast Marching Square + Optimization at ITER scenario.

In collaboration with my friends from the Instituto de Plasmas e Fusão Nuclear, we have appied FM2 to the International Thermonuclear Experimental Reactor and carried out a very exhaustive analysis. The results were very good: the FM2 properties fit very well in this problem. An optimization procedure is applied after FM2 in order to make the path even smoother and check that the ITER requirements are satisfied.

Fast Marching Learning

FM2 computes trajectories that are far from obstacles. In other words, the paths go through the high velocity zones. The following question seems obvious: why not to deliberately modify the velocities map so we can guide the trajectory?

Therefore, given a previous path (experience), the Fast Marching Learning (FML) algorithm is able to:

  • Reproduce the experience, so that new paths will imitate previous paths.
  • Boost the computation time, since now the FMM wave is directed through an specific path.
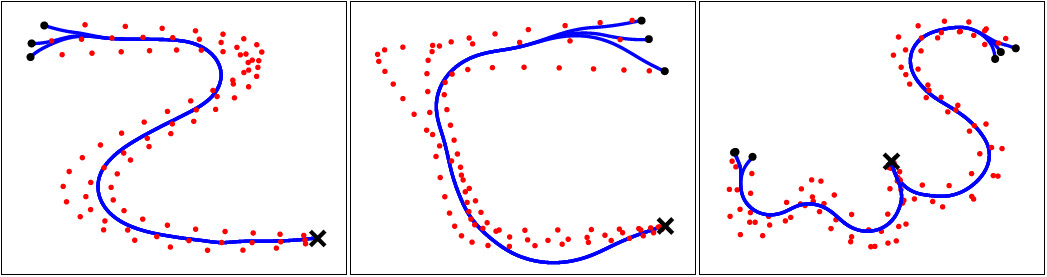
Fast Marching Method

Fast Marching Learning applied to handwriting motions.

If a regular planner is applied, the output would be (kind of) straight lines between points. In this case, FML (blue paths) follows the previous experience (red points).

Multirobot formation motion planning with Fast Marching Square

It turns out that FM2 is a very good base algorithm for planning robot formations. In this case, a path is computed for the leader. Since it goes far from obstacles, it is easier for the rest of the robots (followers) to follow the leader with a prescribed formation geometry. This geometry, however, is deformed taking into account the velocities map in order to accomodate the formation to the environment. This way, we obtain smooth, safe paths for all the robots in the formation while keeping the geometry as much as possible.

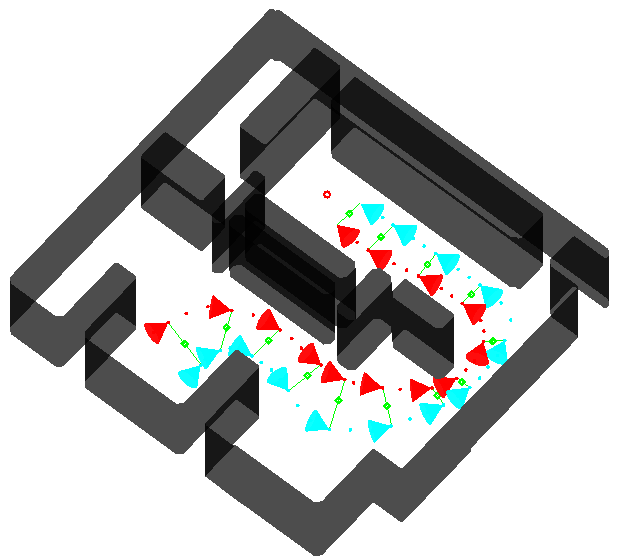
Fast Marching Method

FM2-based robot formation planning.

Grasp Planning

Going deeper into formations, I have participated in modeling a robotic hand using the 3D version of the formation planning algorithm. Every joint is considered as a robot of the formation constrained to a given distance (finger sizes) and limit positions. The results are that we are able to plan for a hand really fast, since we are planning for many 3D robots, instead of for just one high-dimensional robot.

FM2* and FMDirectional

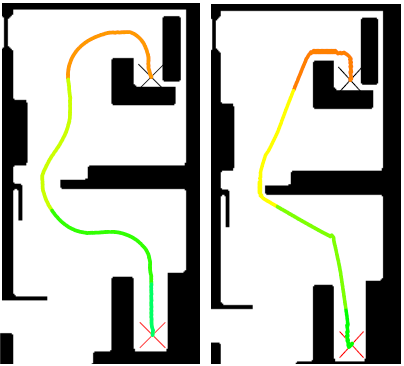
Fast Marching Method

FM2 (left) - FMDirectional (right)

So far, only high-level planning algorithms have been introduced. Here, a cost-to-go heuristic is included so that the FMM is directed towards the goal, decreasing the path computation time, while keeping the same path. Also, we have solved a basic problem of the FM2. Sometimes, it gets far away from obstacles when it is not required. Therefore, FMDirectional improves the path lengths and execution time of the trajectories.

Source code

Note
Not all my research code is available. Just because I don't think it is worthy. Contact me if you are interested anyway.
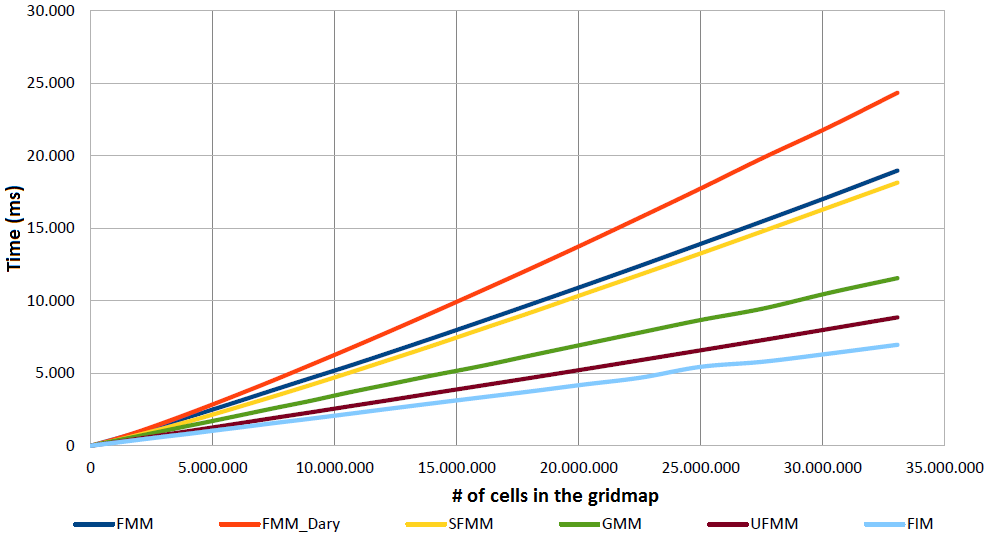
Fast Marching Method

FMM versions comparison.

  • Matlab FM2 source: High level planning algorithms. This code requires the Gabriel Peyré's Fast Marching Toolbox. If have created a small tutorial about how to install this toolbox: FM Toolbox

  • C++ FMM and FM2: n-dimensional Fast Marching Method code with different FMM and FM2 versions implemented and basic tools to test them. You can find a very easy tutorial.

Please, contact me if you have any problem/question about this code.

References

In order to get introduced to the FM2 method, I recommend the following publications:

  • A. Valero, J.V. Gómez, S. Garrido and L. Moreno, The Path to Efficiency: Fast Marching Method for Safer, More Efficient Mobile Robot Trajectories, IEEE Robotics and Automation Magazine, Vol. 20, No. 4, 2013. Impact factor (2013): 2.319, Q1.
    PDF
  • J.V. Gómez Master's Thesis, Advanced Applications of the Fast Marching Square Planning Method, Carlos III University of Madrid, 23rd November, 2012.
    PDF

In my publications you can find the full list.